Reglas para Hacer una Presentación en Power Point


Apoyarse en fundamentos sólidos, robustos.

La herramienta de apoyo Power Point no es más que eso, un apoyo. Por muy atractivas y llamativas que resulten las diapositivas recuerda que lo principal eres tú y el mensaje. Los asistentes a una presentación desean escucharte, no contemplar un espectáculo de diapositivas en una pantalla por muy bien realizadas que estas estén. Construye con argumentos sólidos con los que poder convencer al auditorio, expón ideas contundentes que logren persuadir y conseguirás así realizar entonces una presentación con éxito. Usa muchas transparencias. Son gratis, así que usa todas las que necesites. No intentes “comprimir” una idea compleja en una sola transparencia. Dedica toda una secuencia de ellas, si hace falta, a explicar una sola idea.

Sencillez.

Las presentaciones más eficaces son aquellas con gráficos sencillos y fáciles de comprender con no más de 5 líneas de texto por diapositiva. No satures de información una diapositiva ni incorpores accesorios que no sean imprescindibles. Recuerda que lo más importante, lo imprescindible, es tu discurso, no lo que aparece en la pantalla.
Los tipos de letra como Arial son más legibles que los tipos con serif (como el Times New Roman). Está bien usar tipos de letra originales, pero recuerda que el ordenador en el que vayas a hacer la presentación no tiene por qué tenerlos instalados. Y usa el mismo en toda la presentación, no uno en cada transparencia. Y por supuesto, nunca varios en una misma transparencia. Usa un tipo de letra de al menos 30 puntos. Nunca menos. ¿Qué te cabe poco texto? Pues de eso se trata. Porque eso facilita cumplir las siguiente reglas.

 Incluir solamente las cifras y datos que sean absolutamente imprescindibles.

Resulta difícil transmitir un mensaje de un modo conciso si bombardeamos al espectador con un sinfín de cifras y datos. No abrumes a los asistentes con estadísticas. Siempre puedes distribuir notas o incluso un pequeño informe al final de la presentación para que lo estudien.

 Evitar la lectura literal de diapositivas.

Uno de los hábitos negativos más comunes es limitarse a realizar una lectura al pie de la letra del contenido de la diapositiva. Esto produce unos efectos muy negativos y hace que la presentación acabe aburriendo a los asistentes. Uno de los hábitos más generalizados y perjudiciales de los usuarios de PowerPoint consiste en limitarse a leer la presentación visual a la audiencia. No sólo es redundante (si no es para controlar el mando a distancia, es difícil justificar así la presencia del orador), sino que, además, la presentación más atractiva se hace aburrida. El usar tus transparencias como “teleprompter”. Es la manera más segura de perder a la audiencia: ellos leen más rápido de lo que tú puedes hablar, así que han terminado cuando a ti todavía te falta media transparencia. En ese momento se aburren, se distraen, y se impacientan, pensando en el tiempo que están perdiendo.
Una presentación de PowerPoint resulta más eficaz con comentarios verbales que amplían e interpretan lo que hay en la pantalla en lugar de repetirlo. "Incluso con PowerPoint es necesario el contacto visual con la audiencia". Lo más importante de una presentación eres tú y el mensaje, no el contenido de la diapositiva. Interpreta lo que aparece reflejado en la pantalla, no lo leas. Mantén así un mayor contacto con la audiencia.

 Emplea solamente observaciones oportunas.
 
No realices comentarios que ya aparezcan reflejados en las diapositivas. Deja un tiempo para que los presentes que lean el texto y a continuación expón alguna observación que pueda ampliar su contenido.

 No fatigues a los asistentes.

Emplea ocasionalmente diapositivas en blanco para no sobrecargar de información a los asistentes. De esta forma se conseguirá además lograr una mayor atención del público, lo cual resultaría ser una táctica muy eficaz.

Utiliza el contraste de colores.

Resulta muy eficaz para transmitir emociones el usar un contraste marcado entre el color del texto y el de los gráficos y el fondo.

 Incluye imágenes y gráficos novedosos.

Dale mayor atractivo visual a tus exposiciones incluyendo gráficos e imágenes exportadas. No te limites a utilizar simplemente los recursos que ofrece la herramienta de Power Point. Usa imágenes, pero que sean de calidad. Ni se te ocurra usar el clipart de Office, como todo el mundo, o peor aún, cliparts baratos de los que pululan por Internet. Usa fotografías, que puedes encontrar gratis o muy baratas en sitios como Flickr o Dreamstime. Resulta muy atractivo incluir breves secuencias de video que además de transmitir un mensaje de manera eficaz, amenizan y relajan el ambiente.

 Distribuye notas e informes al final, no durante la presentación.

 A menos que sea imprescindible, no distribuyas documentos en el transcurso de una presentación. Esto hará que desvíen su atención a la lectura de los mismos. Espera a que termine la exposición para distribuirlos.

 No tengas reparos en realizar modificaciones antes de exponer.

No pierdas nunca la perspectiva de la audiencia. Después de confeccionar el borrador de las diapositivas de PowerPoint, imagínate que eres una de las personas que escuchan tus comentarios mientras las repasas. Si algo es poco interesante, distrae o confunde, corrígelo sin pensarlo dos veces. Es muy probable que consigas mejorar la presentación.

Ten a mano tu presentación.

 Muchas veces te la pedirán por adelantado, pero no te fíes pensando que por haberla enviado estará preparada cuando des la charla. Lleva una memoria USB, y cuélgala además en Internet, en un sitio que sea fácilmente accesible (puedes enviártela a tu cuenta de Gmail, por ejemplo. Cualquier cosa que te evite encontrarte a cinco minutos de la presentación sin el apoyo de las transparencias. Lleva una copia en PDF. Si toda falla, si las versiones de los programas son incompatibles, si las imágenes se descuadran, si las letras salen de los cuadros de texto, en lugar de tirarte de los pelos siempre podrás usar la versión en PDF. Y tampoco sería mala idea llevar un lector ligero de PDF, como el Foxit

 Mejor en tu portátil:

Si puedes, es preferible hacer la presentación en tu portátil. Así sabes exactamente cómo va a quedar y evitas problemas de compatibilidad entre versiones, de tipos de letra desaparecidos, de vídeos o sonidos embebidos que no aparecen, de gráficos descuadrados. Si tienes que hacerlo con otro ordenador es conveniente que te cerciores con antelación, acudiendo un poco antes al lugar de la presentación, comprobando que todo funcionará correctamente.

ESTRUCTURA DISCRETA

Lógica matemática

Operadores lógicos. -

1.- and = y: ˄

Proposiciones:

 es toda expresión que tiene o puede decir si es verdadero o falso, es toda expresión que tiene un valor especial.

                                           V

Proposición 

                                           F

Ejemplo:

.) El símbolo de agua es h20

.) la u.p.d.s es una universidad

La proposición se podría decir que es una expresión que puede ser verdadera o falsa, pero a la vez la que no cambia.

A partir de preposiciones simples se pueden generar otras preposiciones simples o compuestas utilizando conectores lógicos tales como:

El conectivo “NO” se denota por “   ͠    “  “ ⌐ “

El conectivo “y “se denota por “˄ “

El conectivo “o “se denota por “˅ “   

                       

El conectivo “si entonces “se denota por “→ “

el conectivo “si y solo si "se denota por “↔ “

el conectivo “o excluyente “se denota por “Ұ “

Operaciones preposicionales. –

.) la negación → “  ͠  “

.) la conjunción → “˄ “

.) la disyunción → “˅ “

.) la implicación → “→ “

.) doble implicación → “↔ “

.) disyunción exclusiva → “Ұ “

.) negación. -

  la negación es aquella que niega a la proposición como “p” en “   ͠    p”   

, a continuación, demostraremos en una tabla de verdad

P	͠    P
V	F
F	V

Ejemplo:

P: EL GATO LADRA	͠     p: EL GATO NO LADRA
Q: 3+4=5	͠  Q: 3+4≠5

.) Conjunción. -

  se llama conjunción a las dos proposiciones “p” y “q” que cuando uniéndolas con el colectivo “Y” que se escribiría “˄” tenemos “p ˄ q”.

Y la regla dice que es verdadera “v” solo cuando las dos proposiciones son verdaderas caso contrario será falso “f “.

Ejemplo:

P	Q
V	V
V	F
F	V
F	F

.) disyunción. – 

se llama disyunción a dos proposiciones “p” y “q” uniéndolas por el colectivo “˅” y se escribe “p ˅ q”

Y la regla dice que es falsa solo cuando las dos proposiciones son falsas en caso contrario es verdadero

Ejemplo:

P	q
V	V
V	F
F	V
F	f

.) implicación. –

se llama implicación a dos proposiciones “p” y “q” uniéndolas por el colectivo “→” y se escribe “p → q”

Y la regla dice que es falso si el antecedente “p” es verdadero y el consecuente “q” es falso caso contrario es verdadero

P	q
V	V
V	F
F	V
F	F

.) doble implicación. - 

se llama doble implicación a dos proposiciones “p” y “q” uniéndolas por el colectivo “↔” y se escribe “p ↔ q”

Y la regla dice que es verdadero es verdadero solo si ambas posiciones tienen el mismo valor caso contrario es falso

Ejemplo:

P	q
V	V
V	F
F	V
F	F

.) Disyunción exclusiva. -

  se llama disyunción exclusiva a dos proposiciones “p” y “q” uniéndolas por el colectivo “Ұ” y se escribe “p Ұ q”

Y la regla dice que es falso si las dos proposiciones tienen el mismo valor caso contrario es verdadero

Ejemplo:

P	q
V	V
V	F
F	V
F	f

Tabla de verdad de todos los colectivos. –

P	q	P ˄ q	P ˅ q	P → q	P ↔ q	P Ұ q
V	V	V	V	V	V	F
V	F	F	V	F	F	V
F	V	F	V	V	F	V
F	F	F	F	V	V	F

Formula proposicional. -  

una forma proposicional es una combinación de proposiciones y colectivos lógicos que simbolizan proposición compuesta.

Ejemplo:

[(p ˅ q) → r] ˄ (p → q)

Ahora veremos cómo se resuelve a través de una tabla de verdad

p	q	r	P ˄  q	(P ˄ q) ˅ r	͠  p	[(p ˄ q) ˅ r] →   ͠   p
V	V	V	F	V	F	F
V	V	F	F	F	F	V
V	F	V	F	V	F	F
V	F	F	F	F	F	V
F	V	V	V	V	V	V
F	V	F	V	V	V	V
F	F	V	V	V	V	V
F	F	F	V	V	V	V

                                                                                                 

Clasificación de fórmulas proposicionales. -

  las formulas proposicionales se clasifican según su valor de verdad en:

Tautología

Contradicción

Contingencia

Tautología. -

forma preposicional que es verdadera para cualquier valor de verdad de las proposiciones que la componen

V

V

V

V

V

V

V

V

Contradicción. -

forma proposicional que es falsa para cualquier de verdad de las proposiciones que la componen

F

F

F

F

F

F

F

F

Contingencia. -

forma proposicional que no es ni tautología ni contingencia

F

V

V

V

F

V

F

V

Ejemplo. -

[(  ͠  p ˅ q) ˄ (q → r )] →   ͠   (p ˄   ͠    r)

p	q	r	͠  p	͠  r	(  ͠   p ˅ q)	(q → r)	[(   ͠  p ˅ q) ˄ (q → r)]	P ˄  ͠   r	͠   (p ˄ r)	p → q
V	V	V	F	F	V	V	V	F	V	V
V	V	F	F	V	V	F	F	V	F	v
V	F	V	F	F	F	V	F	F	V	V
V	F	F	F	V	F	V	F	V	F	V
F	V	V	V	F	V	V	V	F	V	v
F	V	F	V	V	V	F	F	F	V	V
F	F	V	V	F	V	V	V	F	V	V
F	F	F	V	V	V	V	V	F	V	v

                                                                                            Tautología 

Algebra de proposiciones. –

Son operaciones lógicas que se realizan en una forma proposicional aplicando adecuadamente ciertas reglas llamadas leyes lógicas.

Es decir, a igual que el álgebra donde la simplificación de expresiones algebraicas es muy importante y lógicamente también existe la necesidad de simplificar formulas atreves de ciertas equivalencias llamadas leyes lógicas.

Leyes lógicas. -

1.- Ley de la impotencia                                                   2.- leyes conmutativas

P ˄ p ≡ p; p ˅ p ≡ p                                                           p ˄ q ≡ q ˄ p; p ˅ q ≡ q ˅ p

3.- ley asociativa                                                              4.- ley de negación

P ˄ (q ˄ r) ≡ (p ˄ q)                                                           ͠  (  ͠  p) ≡ p

P ˅ (q ˅ r) ≡ (p ˅ q) ˅ r                                                      p ˄  ͠  p ≡ f; p ˅  ͠  p ≡ v

5.- ley de identidad                                                          6.- ley de Morgan

p ˄ v ≡ p; p ˅ f ≡ p                                                            ͠  (p ˅ q) ≡  ͠  p ˄  ͠  q

                                                                                        ͠  (p ˄ q) ≡  ͠  p˅  ͠  q

7.- definición de implicación                                           8.- ley distributiva

p → q ≡  ͠  p ˅ q                                                                 p ˄ (q ˅ r) ≡ (p ˄ q) ˅ (p ˄ r)

  

                                                                                       p ˅ (q ˄ r) ≡ (p ˅ q) ˄ (p ˅ r)

9.- ley de adsorción                                                          10.- definición de doble

P ˄ (p ˅ q) ≡ p / p ˄ f ≡ f                                                   implicación

P ˅ (p ˄ q) ≡ p / p ˅ v ≡ v                                                  p ↔ q ≡ (p → q) ˄ (q → p)

11.- definición disyunción exclusiva

P Ұ q ≡  ͠  (p ↔ q)

simplificación de fórmulas proposicionales se trata de expresar o transformar una formula proposicional en otras equivalentes a ella, pero lo más reducida posible. para lo cual se debe usar una de las leyes lógicas.

así mismo deben especificarse en cada paso la ley que fueron utilizados 

ejemplo:

͠  (p →  ͠  q) ˄ p ≡  ͠  (  ͠  p ˅   ͠  q) ˄ p                                    definición de implicación

≡ [  ͠  (  ͠  p) ˄  ͠  (  ͠  q)] ˄ p                                             ley de Morgan

≡ [p ˄ q] ˄ p                                                                      ley de negación

≡ (p ˄ p) ˄ q                                                                      ley asociativa

≡ p ˄ q                                                                              ley de impotencia

Circuitos lógicos. -

Un circuito es un interruptor que puede estar abierto o cerrado

Si asociamos una proposición aun interruptora intuitivamente vemos que en el álgebra de circuitos la v que se significaría de verdadero de tal proposición que indica que el interruptor está encerrado y f que significaría falso indica que el interruptor esta abierto

Podemos representar de forma gráfica una proposición.

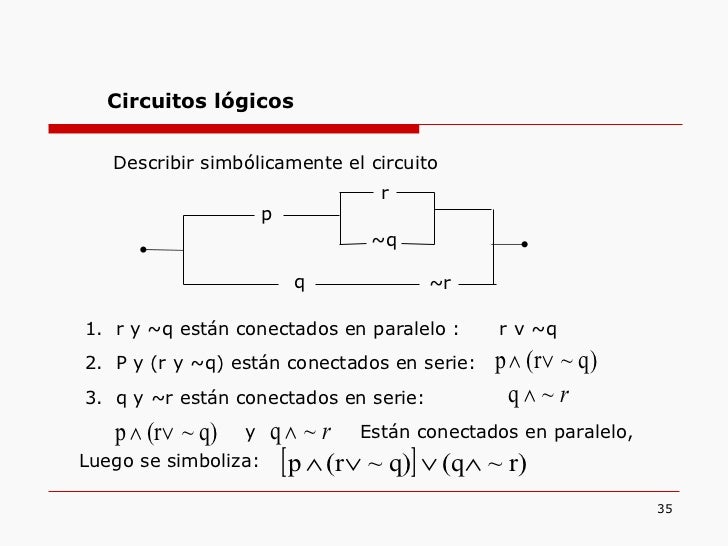
ejemplo:

interferencia lógica.-

Dado que no siempre es factible construir una tabla de verdad para comprobar la validez de un razonamiento (cuando el numero de proposiciones es elevado, la tabla puede ser excesivamente larga), utilizaremos únicamente el procedimiento de probar que se da la implicación lógica.

Diremos que la proposicional Q se infiere de las proposiciones P1, P2, . . . , Pn si Q es verdad cuando todas las Pi , i = 1, 2, . . . , n lo sean, es decir, cuando P1 ∧ P2 ∧ · · · ∧ Pn =⇒ Q. Obs´ervese que esto es lo mismo que decir que el razonamiento P1 ∧ P2 ∧ · · · ∧ Pn −→ Q sea v´alido. La escribiremos en la forma siguiente:

P1 

P2 

. 

. 

.

 Pn 

 Q

MODUS PONENDO PONENS (PP)

            p → q             “Si llueve, entonces las calles se mojan”        (premisa)

            p                   “Llueve”                                                    (premisa)

__________________________________________________

            q                      “Luego, las calles se mojan”                         (conclusión)

           

            El condicional o implicación es aquella operación que establece entre dos enunciados una relación de causa-efecto. La regla ‘ponendo ponens’ significa, “afirmando afirmo” y en un condicional establece, que si el antecedente (primer término, en este caso p) se afirma, necesariamente se afirma el consecuente (segundo término, en este caso q).

            MODUS TOLLENDO TOLLENS (TT)

            ‘Tollendo tollens’ significa “negando, niego”, y se refiere a una propiedad inversa de los condicionales, a los que nos referíamos en primer lugar.

           

               p → q             “Si llueve, entonces las calles se mojan”    

            ¬q                      “Las calles no se mojan”                                                                

__________________________________________________

            ¬p                      “Luego, no llueve”

            Si de un condicional, aparece como premisa el consecuente negado (el efecto), eso nos conduce a negar el antecedente (la causa), puesto que si un efecto no se da, su causa no ha podido darse.

            Esto nos permite formular una regla combinada de las ambas anteriores, consecuencia ambas de una misma propiedad de la implicación; la regla ponendo ponens sólo nos permite afirmar si está afirmado el antecedente (el primer término de la implicación), y la regla tollendo tollens sólo nos permite negar a partir del consecuente (segundo término de la implicación); ambas consecuencias se derivan de que la implicación es una flecha que apunta en un único sentido, lo que hace que sólo se pueda afirmar a partir del antecedente y negar sólo a partir del consecuente.

            DOBLE NEGACIÓN (DN)

            ¬¬p ↔ p

            El esquema representa, “p doblemente negada equivale a p”. Siguiendo el esquema de una inferencia por pasos, la representaríamos así:

            ¬¬p                “No ocurre que Ana no es una estudiante”

_____________________________________________________

                 p                 “Ana es una estudiante”

           

            La regla ‘doble negación’, simplemente establece que si un enunciado está doblemente negado, equivaldría al enunciado afirmado.

            ADJUNCIÓN Y SIMPLIFICACIÓN

            Adjunción (A): Si disponemos de dos enunciados afirmados como dos premisas separadas, mediante la adjunción, podemos unirlos en una sola premisa utilizando el operador Λ (conjunción).

           

p          “Juan es cocinero”

           

q          “Pedro es policía”

            ___________________________________

p Λ q   “Juan es cocinero y Pedro es policía”

            Simplificación (S): obviamente, es la operación inversa. Si disponemos de un enunciado formado por dos miembros unidos por una conjunción, podemos hacer de los dos miembros dos enunciados afirmados por separado.

p Λ q               “Tengo una manzana y tengo una pera”

____________________________________________

p                      “Tengo una manzana”

q                      “Tengo una pera”

MODUS TOLLENDO PONENS (TP)

            La disyunción, que se simboliza con el operador V, representa una elección entre dos enunciados. Ahora bien, en esa elección, forma parte de las posibilidades escoger ambos enunciados, es decir, la verdad de ambos enunciados no es incompatible, si bien, ambos no pueden ser falsos.

            A partir de lo anterior, se deduce la siguiente regla, denominada tollendo ponens (negando afirmo): si uno de los miembros de una disyunción es negado, el otro miembro queda automáticamente afirmado, ya que uno de los términos de la elección ha sido descartado.

              p V q                         “He ido al cine o me he ido de compras”

            ¬q                               “No he ido de compras”

__________________________________________________________

              p                               “Por tanto, he ido al cine”

           

            LEY DE LA ADICIÓN (LA)

            Dado un enunciado cualquiera, es posible expresarlo como una elección (disyunción)  acompañado por cualquier otro enunciado.

           

            a                                  “He comprado manzanas”

______________________________________________________________

            a V b                           “He comprado manzanas o he comprado peras”

            SILOGISMO HIPOTÉTICO (SH)

            Dados dos implicaciones, de las cuales, el antecedente de la una sea el consecuente de la otra (el mismo enunciado), podemos construir una nueva implicación cuyo antecedente sea el de aquella implicación cuya consecuencia sea el antecedente de la otra implicación, y cuyo consecuente sea el de ésta última, cuyo antecedente era consecuencia del primero.

            Expresado de otro modo, si una causa se sigue una consecuencia, y ésta consecuencia es a su vez causa de una segunda consecuencia, se puede decir que esa primera causa es causa de esa segunda consecuencia, del mismo modo que, si una bola de billar roja golpea a otra bola blanca que a su vez golpea a una bola negra, la bola roja es causa del movimiento de la bola negra. Expresado en forma de inferencia lógica:

           

            p → q              “Si la bola roja golpea a la bola blanca, la bola blanca se mueve”

            q → r              “Si la bola blanca golpea a la bola negra, la bola negra se mueve”

______________________________________________________________________

           

            p → r              “Si la bola roja golpea a la bola blanca, la bola negra se mueve”

             SILOGISMO DISYUNTIVO (DS)

            Dadas tres premisas, dos de ellas implicaciones, y la tercera una disyunción cuyos miembros sean los antecedentes de los condicionales, podemos concluir en una nueva premisa en forma de disyunción, cuyos miembros serían los consecuentes de las dos implicaciones. Lógicamente, si planteamos una elección entre dos causas, podemos plantear una elección igualmente entre sus dos posibles efectos, que es el sentido de esta regla.

             p → q             “Si llueve, entonces las calles se mojan”

             r →  s             “Si la tierra tiembla, los edificios se caen”

             p V  r              “Llueve o la tierra tiembla”

____________________________________________________

            q V  s              “Las calles se mojan o los edificios se caen”

  

      SIMPLIFICACIÓN  DISYUNTIVA (SD)

            Si disponemos de dos premisas que corresponden a dos implicaciones con el mismo consecuente, y sus antecedentes se corresponden con los dos miembros de una disyunción, podemos concluir con el consecuente de ambas implicaciones.

            p V q               “Helado de fresa o helado de vainilla”

            p → r              “Si tomas helado de fresa, entonces repites”

            q → r              “Si tomas helado de vainilla, entonces repites”

           

____________________________________________________

            r                      Luego, repites

           

            LEY CONMUTATIVA

            Esta ley, no es válida para la implicación, pero sí para conjunción y para la disyunción. Una conjunción es afirmar que se dan dos cosas a la vez, de modo que el orden de sus elementos no cambia este hecho. Igualmente, una disyunción es presentar una elección entre dos cosas, sin importar en qué orden se presente esta elección. Así pues,

            p Λ q ↔ q Λ p            “«p y q» equivale a «q y p»”

            p V q ↔ q V p             “«p ó q» equivale a «q ó p»

            LEYES DE MORGAN (DM)

            Esta ley permite transformar una disyunción en una conjunción, y viceversa, es decir, una conjunción en una disyunción. Cuando se pasa de una a otra, se cambian los valores de afirmación y negación de los términos de la disyunción/conjunción así como de la propia operación en conjunto, como podemos observar aquí:

      p Λ q                                p V q

___________                 ____________      

 ¬(¬p V ¬q)                        ¬(¬p Λ ¬q)

 Función Proposicional.-

Supongamos los enunciados abiertos: 

" x es la capital de Buenos Aires"

" y + 4 = 11"

Estos no tienen un valor veritativo. Pero si en el primero de ellos hacemos x = La Plata, tenemos:

"La Plata es la capital de Buenos Aires" (V)

Asimismo, si en el segundo hacemos x = 9, resulta:  9 + 4 = 11 (F)

Podemos, entonces, dar la siguiente definición: "Una función proposicional es un enunciado abierto de la forma P_(x) que se convierte en una proposición cuando se le asigna un valor específico a la variable".

Ejemplos:

p_(x) : 2x + 5 > 11 , si x = 4 \ 13 > 11 (Verdadero)

q_(x) : 3x + 7 = 11 , si x = 5 \ 22 = 16 (Falso)

r_(x) : 2x + 1 = 5 , si x = 2 \ 5 = 5 (Verdadero)

s_(x) : x es un animal, si x = mesa se tendrá : mesa es un animal (Falso)

t_(x) : x es un ave, si x = flamenco se tiene: el flamenco es un ave (Verdadero)

Cuantificadores

A partir de funciones proposicionales es posible obtener proposiciones generales mediante un proceso llamado de cuantificación. Asociados a la indeterminada x, introducimos los símbolos " x y $ x, llamados cuantificador universal y cuantificador existencial respectivamente. Las expresiones

Para todo x, se verifica p_(x) se denota por " x : p_(x)

Existe x, tal que se verifica p_(x) se denota por $ x / p_(x)

Corresponden a una función proposicional p_(x) cuantificada universalmente en el primer caso, y existencialmente en el segundo.

Ejemplo: Una función proposicional cuantificada universalmente es V si y sólo si son V todas las proposiciones particulares asociadas a aquella. Para asegurar la verdad de una proposición cuantificada universalmente es suficiente que sea verdadera alguna de las proposiciones asociadas a la función proposicional.

Un problema de interés es la negación de funciones proposicionales cuantificadas. Por ejemplo, La negación de "Todos los enteros son impares" es "Existen enteros que no son impares"   y en símbolos: $ x / ~ p_(x)

Entonces, para negar una función proposicional cuantificada universalmente se cambia el cuantificador en existencial, y se niega la función proposicional.

Ejemplo:  Supongamos la proposición: Todos los alumnos de mi colegio son aplicados

La vamos a escribir en lenguaje simbólico, negarla y retraducir la negación al lenguaje ordinario.

Nos damos cuenta pronto que se trata de la implicación de dos funciones proposicionales:

p_(x) : es alumno de mi colegio

q_(x) : es aplicado

Tenemos:  " x : p_(x) Þ q_(x)

Teniendo en cuenta la forma de negar una función proposicional cuantificada universalmente y una implicación resulta:

$ x / p_(x) Ù ~ q_(x)